travelling sales person problem in c

Data Structures & Algorithms
DSA - Overview
DSA - Environment Setup
DSA - Algorithms Basics
DSA - Asymptotic Analysis
Data Structures
DSA - Data Structure Basics
DSA - Data Structures and Types
DSA - Array Data Structure
Linked Lists
DSA - Linked List Data Structure
DSA - Doubly Linked List Data Structure
DSA - Circular Linked List Data Structure
Stack & Queue
DSA - Stack Data Structure
DSA - Expression Parsing
DSA - Queue Data Structure
Searching Algorithms
DSA - Searching Algorithms
DSA - Linear Search Algorithm
DSA - Binary Search Algorithm
DSA - Interpolation Search
DSA - Jump Search Algorithm
DSA - Exponential Search
DSA - Fibonacci Search
DSA - Sublist Search
DSA - Hash Table
Sorting Algorithms
DSA - Sorting Algorithms
DSA - Bubble Sort Algorithm
DSA - Insertion Sort Algorithm
DSA - Selection Sort Algorithm
DSA - Merge Sort Algorithm
DSA - Shell Sort Algorithm
DSA - Heap Sort
DSA - Bucket Sort Algorithm
DSA - Counting Sort Algorithm
DSA - Radix Sort Algorithm
DSA - Quick Sort Algorithm
Graph Data Structure
DSA - Graph Data Structure
DSA - Depth First Traversal
DSA - Breadth First Traversal
DSA - Spanning Tree
Tree Data Structure
DSA - Tree Data Structure
DSA - Tree Traversal
DSA - Binary Search Tree
DSA - AVL Tree
DSA - Red Black Trees
DSA - B Trees
DSA - B+ Trees
DSA - Splay Trees
DSA - Tries
DSA - Heap Data Structure
DSA - Recursion Algorithms
DSA - Tower of Hanoi Using Recursion
DSA - Fibonacci Series Using Recursion
Divide and Conquer
DSA - Divide and Conquer
DSA - Max-Min Problem
DSA - Strassen's Matrix Multiplication
DSA - Karatsuba Algorithm
Greedy Algorithms
DSA - Greedy Algorithms
DSA - Travelling Salesman Problem (Greedy Approach)
DSA - Prim's Minimal Spanning Tree
DSA - Kruskal's Minimal Spanning Tree
DSA - Dijkstra's Shortest Path Algorithm
DSA - Map Colouring Algorithm
DSA - Fractional Knapsack Problem
DSA - Job Sequencing with Deadline
DSA - Optimal Merge Pattern Algorithm
Dynamic Programming
DSA - Dynamic Programming
DSA - Matrix Chain Multiplication
DSA - Floyd Warshall Algorithm
DSA - 0-1 Knapsack Problem
DSA - Longest Common Subsequence Algorithm
DSA - Travelling Salesman Problem (Dynamic Approach)
Approximation Algorithms
DSA - Approximation Algorithms
DSA - Vertex Cover Algorithm
DSA - Set Cover Problem
DSA - Travelling Salesman Problem (Approximation Approach)
Randomized Algorithms
DSA - Randomized Algorithms
DSA - Randomized Quick Sort Algorithm
DSA - Karger’s Minimum Cut Algorithm
DSA - Fisher-Yates Shuffle Algorithm
DSA Useful Resources
DSA - Questions and Answers
DSA - Quick Guide
DSA - Useful Resources
DSA - Discussion
Selected Reading
UPSC IAS Exams Notes
Developer's Best Practices
Questions and Answers
Effective Resume Writing
HR Interview Questions
Computer Glossary

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

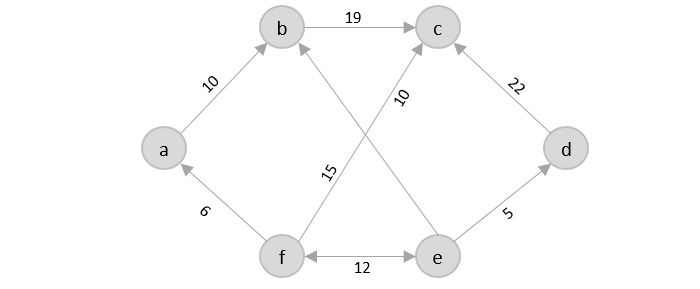
There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

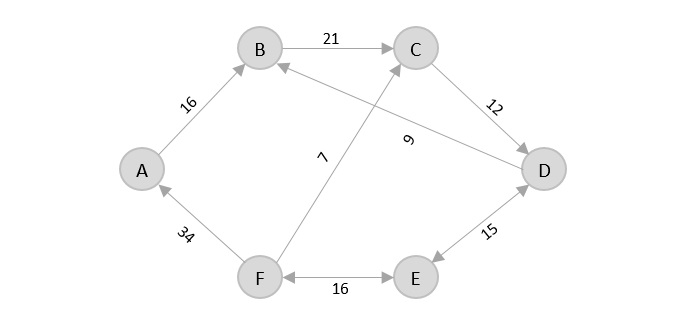
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

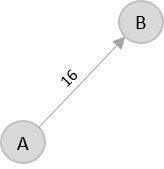
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

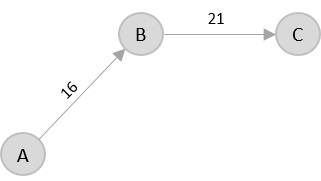
There’s only one edge between C → D, therefore it is added to the output graph.

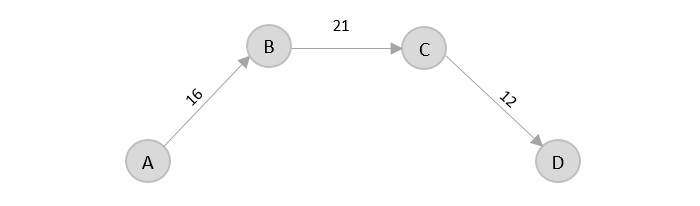
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

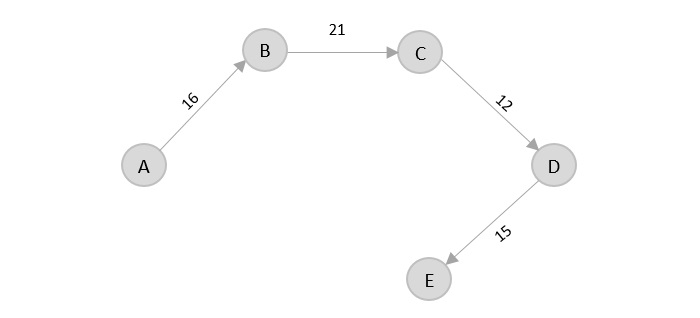
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

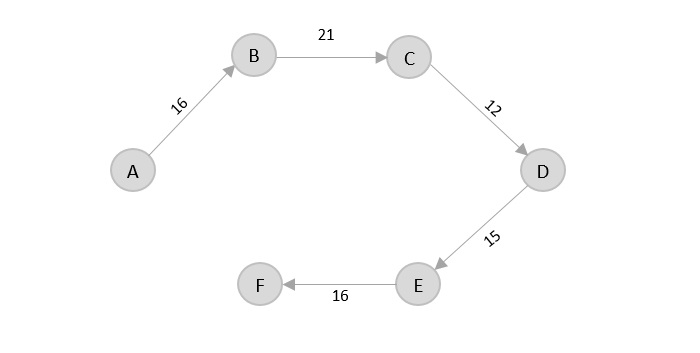
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

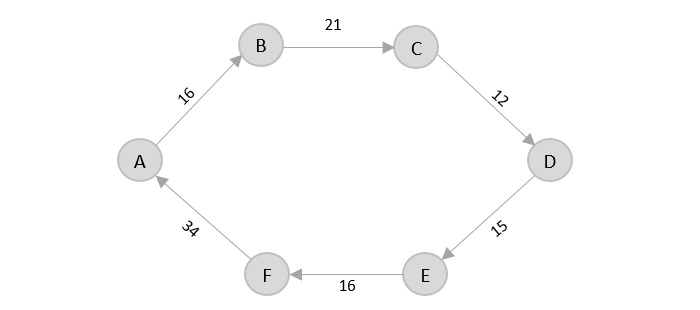
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

Interview Problems on DP
Practice DP
Tutorial on Dynamic Programming
Optimal Substructure
Overlapping Subproblem
Memoization
Tabulation vs Memoization
0/1 Knapsack
Unbounded Knapsack
Coin Change
Egg Dropping Puzzle
Matrix Chain Multiplication
Palindrome Partitioning
DP on Arrays
DP with Bitmasking
DP on Trees
DP on Graph

Travelling Salesman Problem using Dynamic Programming

Travelling Salesman Problem (TSP):

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.

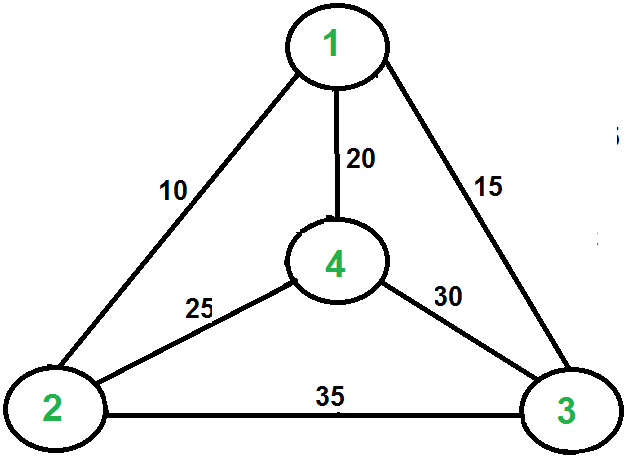
For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem.

Naive Solution:

1) Consider city 1 as the starting and ending point.

2) Generate all (n-1)! Permutations of cities.

3) Calculate the cost of every permutation and keep track of the minimum cost permutation.

4) Return the permutation with minimum cost.

Time Complexity: ?(n!)

Dynamic Programming:

Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex I (other than 1), we find the minimum cost path with 1 as the starting point, I as the ending point, and all vertices appearing exactly once. Let the cost of this path cost (i), and the cost of the corresponding Cycle would cost (i) + dist(i, 1) where dist(i, 1) is the distance from I to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far.

Now the question is how to get cost(i)? To calculate the cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems.

Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i . We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on. Note that 1 must be present in every subset.

Below is the dynamic programming solution for the problem using top down recursive+memoized approach:-

For maintaining the subsets we can use the bitmasks to represent the remaining nodes in our subset. Since bits are faster to operate and there are only few nodes in graph, bitmasks is better to use.

For example: –

10100 represents node 2 and node 4 are left in set to be processed

010010 represents node 1 and 4 are left in subset.

NOTE:- ignore the 0th bit since our graph is 1-based

Time Complexity : O(n 2 *2 n ) where O(n* 2 n) are maximum number of unique subproblems/states and O(n) for transition (through for loop as in code) in every states.

Auxiliary Space: O(n*2 n ), where n is number of Nodes/Cities here.

For a set of size n, we consider n-2 subsets each of size n-1 such that all subsets don’t have nth in them. Using the above recurrence relation, we can write a dynamic programming-based solution. There are at most O(n*2 n ) subproblems, and each one takes linear time to solve. The total running time is therefore O(n 2 *2 n ). The time complexity is much less than O(n!) but still exponential. The space required is also exponential. So this approach is also infeasible even for a slightly higher number of vertices. We will soon be discussing approximate algorithms for the traveling salesman problem.

Next Article: Traveling Salesman Problem | Set 2

References:

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

Check the length of every possible route, one route at a time.
Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

Visit every city.
The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

Time complexity for checking all routes versus running a greedy algorithm and finding a near-optimal solution instead.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.